이진탐색 (Binary Search)
탐색
- 순차 탐색 (Sequential Search): 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법이다. 구현이 쉽고 시간이 충분하다면 항상 원하는 원소를 찾을 수 있다는 장점이 있다. 리스트 내에서 특정한 값의 원소가 있는지 확인하거나 특정한 값을 가지는 원소의 개수를 세는 count() 메소드를 사용할 때도 내부적으로 순차 탐색이 수행된다.
- 최악의 경우 시간 복잡도: O(N)
- 이진 탐색 (Binary Saerch): 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이다. 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하기 때문에 데이터를 매우 빠르게 찾을 수 있다는 특징이 있다. 탐색 시 위치를 나타내는 변수 3개를 사용하는데 탐색하고자 하는 범위의 시작점, 끝점, 중간점이다. 찾고자하는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는다.
- 시간 복잡도: O(logN)
- 구현 방식: 재귀함수, 반복문
트리 자료구조
노드와 노드의 연결로 표현하면 여기에서 노드는 정보의 단위로서 어떠한 정보를 가지고 있는 개체로 이해할 수 있다. 데이터베이스는 내부적으로 대용량 데이터 처리에 적합한 트리 자료구조를 이용하여 항상 데이터가 정렬되어 있다. 트리 자료 구조는 아래와 같이 몇 가지 주요한 특징이 있다
- 트리는 부모 노드와 자식 노드의 관계로 표현된다.
- 트리의 최상단 노드를 루트 노드라고 한다.
- 트리의 최하단 노드를 단말 노드라고 한다.
- 트리에서 일부를 떼어내도 트리 구조이며 이를 서브 트리라고 한다.
- 트리는 파일 시스템과 같이 계층적이고 정렬된 데이터를 다루기에 적합하다.
이진 탐색 트리
트리 자료 구조 중에서 가장 간단한 형태로 이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조이다. 모든 트리가 이진 탐색 트리는 아니며 이진 트리는 아래와 같은 특징을 가진다.
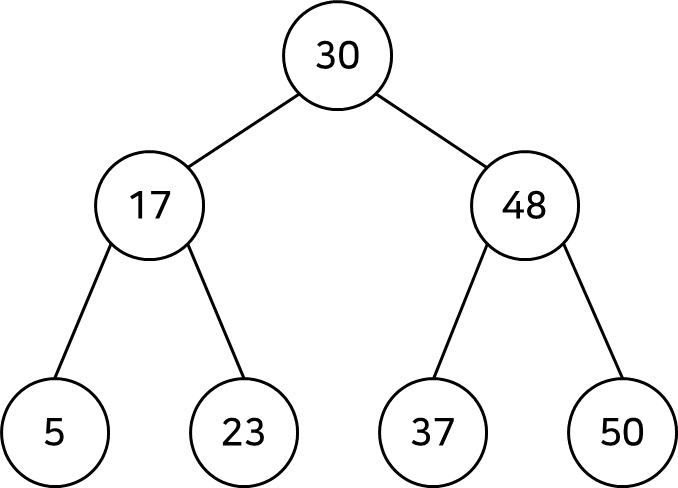
- 부모 노드보다 왼쪽 자식 노드가 작다.
- 부모 노드보다 오른쪽 자식 노드가 크다.
이진 탐색(재귀함수)
import java.util.*;
public class Main
{
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int target = scan.nextInt();
// 정렬된 원소 입력받기
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = scan.nextInt();
}
int result = binarySearch(arr, target, 0, n - 1);
if (result == -1) {
System.out.println(String.format("[%s] doesn't exit.", target));
} else {
System.out.println(result + 1);
}
}
public static int binarySearch(int arr[], int target, int start, int finish){
if(finish <= start) return -1;
int mid = (start + finish) / 2;
if (arr[mid] == target) return mid;
// 검색 대상이 중간값모다 작을 경우 왼쪽은 그렇지 않을 경우 오른쪽을 검색
if(target < arr[mid]) {
return binarySearch(arr, target, start, mid -1);
} else {
return binarySearch(arr, target, mid +1, finish);
}
}
}
이진 탐색(반복문)
import java.util.*;
public class Main
{
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int target = scan.nextInt();
// 정렬된 원소 입력받기
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = scan.nextInt();
}
int start = 0;
int finish = n - 1;
int result = -1;
while(start <= finish){
int mid = (start + finish) / 2;
if(target == arr[mid]) {
result = mid;
break;
} else if(target < arr[mid]) {
finish = mid -1;
} else {
start = mid + 1;
}
}
if (result == -1) {
System.out.println(String.format("[%s] doesn't exit.", target));
} else {
System.out.println(result + 1);
}
}
}
예제 1 - 부품 찾기
난이도 ●◐○ | 풀이 시간 30분 | 시간 제한 1초 | 메모리 제한 128MB
동빈이네 전자 매장에는 부품이 N개 있다. 각 부품은 정수 형태의 고유한 번호가 있다. 어느 날 손님이 M개의 종류의 부품을 대량으로 구매하겠다며 당일 날 견적서를 요청했다. 동빈이는 때를 놓치지 않고 손님이 문의한 부품 M개 종류를 모두 확인해서 견적서를 작성해야 한다. 이때 가게 안에 부품이 모두 있는지 확인하는 프로그램을 작성해보자.
예를 들어 가게의 부품이 총 5개일 때 부품 번호가 다음과 같다고 하자.
N=5
[8, 3, 7, 9, 2]손님은 총 3개의 부품이 있는지 확인 요청했는데 부품 번호는 다음과 같다.
M=3
[5, 7, 9]이때 손님이 요청한 부품 번호의 순서대로 부품을 확인해 부품이 있으면 yes를, 없으면 no를 출력한다. 구분은 공백으로 한다.
입력 조건
- 첫째 줄에 정수 N이 주어진다. (1 <= N <= 1,000,000)
- 둘째 줄에는 공백으로 구분하여 N개의 정수가 주어진다. 이때 정수는 1보다 크고 1,000,000 이하이다.
- 셋째 줄에는 정수 M이 주어진다. (1 <= M <= 100,000)
- 넷째 줄에는 공백으로 구분하여 M개의 정수가 주어진다. 이때 정수는 1보다 크고 1,000,000 이하이다.
출력 조건
- 첫째 줄에 공백으로 구분하여 각 부품이 존재하면 yes를, 없으면 no를 출력한다.
입력/출력 예시
| 입력 예시 | 출력 예시 |
| 5 8 3 7 9 2 3 5 7 9 |
no yes yes |
요점
- 입력 가능한 데이터가 다량이기 때문에 검색은 이진 탐색 알고리즘을 사용하는 것이 효과적
- 이진 탐색이 아닌 계수 정렬과 Set 자료 구조를 활용할 수 있음
소스 코드
import java.util.*;
public class Main
{
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[] parts = new int[n];
for (int i = 0; i < n; i++) {
parts[i] = scan.nextInt();
}
// 부품 목록 오름차순 정렬
Arrays.sort(parts);
int m = scan.nextInt();
int[] targets = new int[m];
for (int i = 0; i < m; i++) {
targets[i] = scan.nextInt();
}
for (int target : targets) {
System.out.print(binarySearch(parts, target) + " ");
}
}
public static String binarySearch(int[] parts, int target){
int start = 0;
int finish = parts.length - 1;
int result = -1;
while(start <= finish){
int mid = (start + finish) / 2;
if(target == parts[mid]) {
result = mid;
break;
} else if(target < parts[mid]) {
finish = mid -1;
} else {
start = mid + 1;
}
}
return (result != -1 ? "yes" : "no");
}
}
예제 2 - 떡볶이 떡 만들기
난이도 ●●○ | 풀이 시간 40분 | 시간 제한 2초 | 메모리 제한 128MB
오늘 동빈이는 여행 가신 부모님을 대신해서 떡집 일을 하기로 했다. 오늘은 떡볶이 떡을 만드는 날이다. 동빈이네 떡볶이 떡은 재밌게도 떡볶이 떡의 길이가 일정하지 않다. 대신에 한 봉지 안에 들어가는 떡의 총 길이는 절단기로 잘라서 맞춰준다.
절단기에 높이 H를 지정하면 줄지어진 떡을 한 번에 절단한다. 높이가 H보다 긴 떡은 H위의 부분이 잘릴 것이고, 낮은 떡은 잘리지 않는다.
예를 들어 높이가 19, 14, 10, 17cm인 떡이 나란히 있고 절단기를 높이를 15cm로 지정하면 자른 뒤 떡의 높이는 15, 14, 10, 15cm가 될 것이다. 잘린 떡의 길이는 차례대로 4, 0, 0, 2cm이다, 손님은 6cm만큼의 길이를 가져간다.
손님이 왔을 때 요청한 총 길이가 M일 때, 적어도 M만큼의 떡을 얻기 위해 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.
입력 조건
- 첫째 줄에 떡의 개수 N과 요청한 떡의 길이 M이 주어진다. (1 <= N <= 1,000,000, 1 <= M <= 2,000,000,000)
- 둘째 줄에는 떡의 개별 높이가 주어진다. 떡 높이의 총합은 항상 M 이상이므로, 손님은 필요한 양만큼 떡을 사갈 수 있다.
- 높이는 10억보다 작거나 같은 양의 정수 또는 0이다.
출력 조건
- 적어도 M만큼의 떡을 집에 가져가기 위해 절단기에 설정할 수 있는 높이의 최댓값을 출력한다.
입력/출력 예시
| 입력 예시 | 출력 예시 |
| 4 6 19 15 10 17 |
15 |
요점
- 절단기의 높이는 0부터 10억까지이기 때문에 제한 시간 내에 해결하려면 이진 탐색을 떠올려야 한다.
- 절단기 높이의 최대 길이는 가장 긴 떡볶이 떡의 길이이다. (탐색범위는 0부터 가장 긴 떡볶이 길이)
- 절단기 높이를 조정하면서 떡의 길이가 M보다 부족하면 절단기 높이를 줄이고 반대일 경우 늘린다.
소스 코드
import java.util.*;
public class Main
{
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int[] riceCakes = new int[n];
for (int i = 0; i < n; i++) {
riceCakes[i] = scan.nextInt();
}
int result = binarySearch(riceCakes, m);
if(result == -1){
System.out.println("Impossible");
} else {
System.out.println("result = " + result);
}
}
public static int binarySearch(int[] riceCakes, int total){
int start = 0;
int finish = Arrays.stream(riceCakes).max().getAsInt();
int result = -1;
while(start <= finish){
int mid = (start + finish) / 2;
int cutTotal = 0;
for(int riceCake : riceCakes){
if (riceCake > mid){
cutTotal += (riceCake - mid);
}
}
if(total == cutTotal) {
result = mid;
break;
} else if(total < cutTotal) {
start = mid + 1;
} else {
finish = mid -1;
}
}
return result;
}
}
이진 탐색 예제를 풀어본 후
정렬을 해야 한다는 부담감이 있지만 정렬이 되어 있다는 전제 조건 하에 O(logN)이라는 시간 복잡도를 가지는 이진 탐색은 굉장히 매력적인 탐색 방법인 것 같다. 범위를 줄여가면서 탐색한다는 점에서 퀵 정렬과 비슷한 부분이 있어서 정렬을 공부한 후 이진 탐색 로직을 짜보니 수월하게 작성할 수 있었고 예제도 큰 고민 없이 괜찮게 풀 수 있었다. 코딩 테스트를 풀 때 입력 조건의 범위를 보기만 하고 크게 신경을 안 썼던 것 같은데 어떤 알고리즘을 써야 할지 결정하는데 큰 힌트가 된다는 것을 이진 탐색 예제를 풀어본 후 알게 되었다.
GitHub: https://github.com/Leeyeonjae/coding-test/tree/main/7_BinarySearch
참고서적 : 이것이 취업을 위한 코딩 테스트다 with 파이썬 by 나동빈
