최단 경로(Shortest Path)
개요
가장 짧은 경로를 찾는 알고리즘으로 '길 찾기' 문제라고도 부른다. 최단 경로 문제는 보통 그래프를 이용하여 표현하는데 각 지점은 그래프에서 '노드(Node)'로 표현되고, 지점 간 연결된 도로는 그래프에서 '간선'으로 표현된다. 또한 실제 코딩 테스트에서는 최단 경로를 모두 출력하는 문제보다는 단순히 최단 거리를 출력하도록 요구하는 문제가 많이 출제된다.

최단 경로 알고리즘에는 그리디 알고리즘과 다이나믹 알고리즘이 적용된다는 특징이 있어 두 알고리즘의 한 유형으로 볼 수 있다. 컴퓨터공학과 학부에서 사용하는 최단 거리 알고리즘은 다익스트라 최단 경로 알고리즘, 플로이드 워셜, 벨만 포드 알고리즘으로 총 3가지지만 코딩 테스트에 주로 등장하는 알고리즘에서 벨만 포드 알고리즘은 제외된다.
다익스트라(Dijkstra) 최단 경로 알고리즘
그래프에서 여러 개의 노드가 있을 때, 특정한 노드에서 출발하여 다른 노드로 가는 각각의 최단 경로를 구해주는 알고리즘이다. 다익스트라 최단 경로 알고리즘은 '음의 간선'이 없을 때 정상적으로 동작한다. 음의 간선이란 0보다 작은 값을 가지는 간선을 의미하는데, 현실 세계의 길(간선)은 음의 간선으로 표현되지 않으므로 다익스트라 알고리즘은 실제로 GPS 소프트웨어의 기본 알고리즘으로 채택되곤 한다.
다익스트라 최단 경로 알고리즘은 기본적으로 그리디 알고리즘으로 분류된다. 매번 '가장 적은 비용이 적은 노드'를 선택해서 임의의 과정을 반복하기 때문이다. 알고리즘의 원리는 다음과 같다.
- 출발 노드와 도착 노드를 설정한다.
- 최단 거리 테이블을 초기화한다.
- 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택한다.
- 해당 노드를 거쳐 다른 노드로 넘어가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
- 위 과정에서 3과 4번의 과정을 반복한다.
동작 과정은 아래 이미지로 자세히 알아볼 수 있다.
- 초기 상태: 그래프를 준비하고 출발 노드를 설정한다.

- Step 1: 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 1번 노드를 처리한다.

- Step 2: 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 4번 노드를 처리한다.
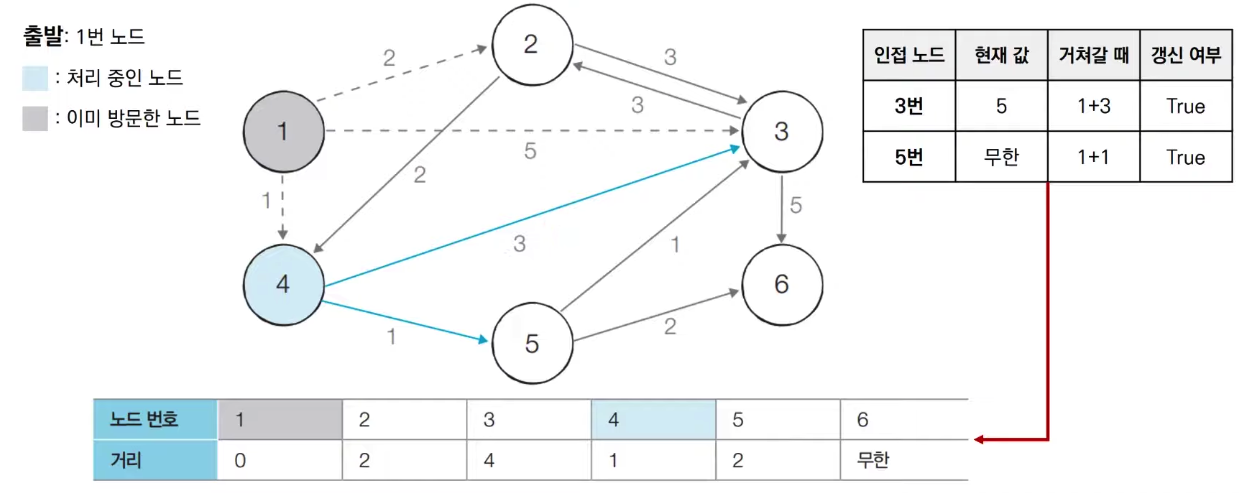
- Step 3: 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 2번 노드를 처리한다.

- Step 4: 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 5번 노드를 처리한다.

- Step 5: 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 3번 노드를 처리한다.

- Step 6: 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 6번 노드를 처리한다.
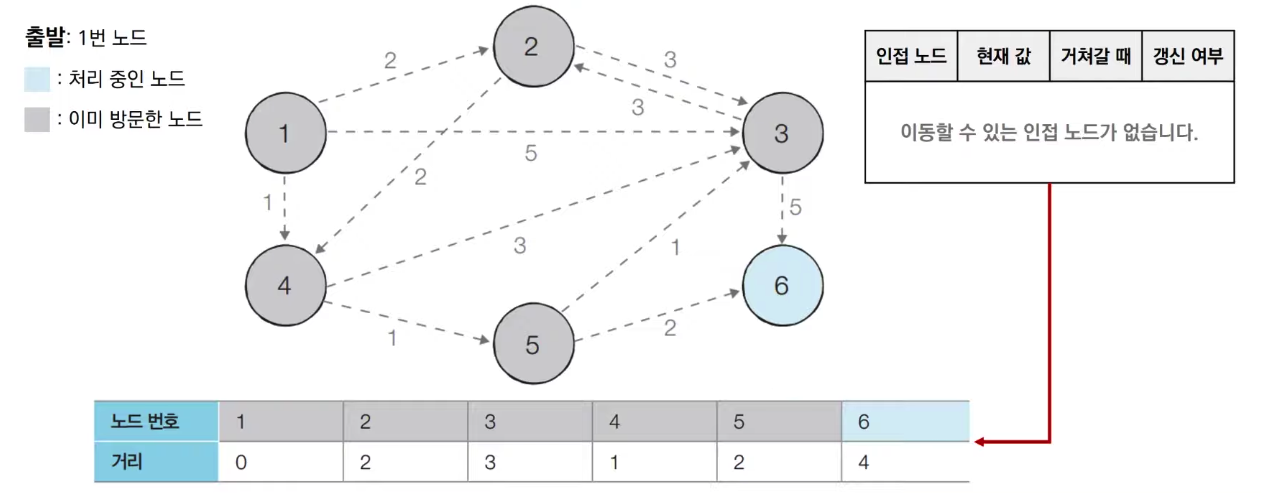
다익스트라를 구현하는 방법은 두 가지가 있다. 구현하기 쉽지만 느리게 동작하는 코드, 구현하기에는 조금 더 까다롭지만 빠르게 동작하는 코드이다. 두 번째 방법으로 기억하고 있는 것이 코딩 테스트에서 조금 더 유용하며 두 방법의 차이는 우선순위 큐 (Priority Queue)의 사용 유무이다.
다익스트라 - 구현하기 쉽지만 느리게 동작하는 코드
노드의 개수가 V일 때 이 방법은 O(V²)의 시간 복잡도를 가진다. 왜냐하면 O(V) 번에 걸쳐서 최단 거리가 가장 짧은 노드를 매번 선형 탐색해야 하고, 현재 노드와 연결된 노드를 매번 일일이 확인해야 하기 때문이다. 따라서 코딩 테스트의 최단 경로 문제에서 전체 노드의 개수가 5,000개 이하라면 일반적으로 이 코드로도 문제를 풀 수 있을 것이다. 하지만 노드의 개수가 10,000개를 넘어가는 문제라면 이 코드로는 문제를 해결하기 어렵다. 노드의 개수 및 간선의 개수가 많을 때는 이어서 설명할 '개선된 다익스트라 알고리즘'을 이용해야 한다.
import java.util.*;
class Node {
int index;
int distance;
public Node(int index, int distance){
this.index = index;
this.distance = distance;
}
public int getIndex() { return this.index; }
public int getDistance() { return this.distance; }
}
public class Main
{
// 방문 정보 저장
private static boolean[] visited;
// 최단 거리 저장
private static int[] shortestPath;
// 간선 연결정보 저장
private static ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
// 무한대 값 상수
private static final int INF = (int) 1e9;
// 노드 개수
private static int nodeCnt;
// 간선 개수
private static int edgeCnt;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
nodeCnt = scan.nextInt();
edgeCnt = scan.nextInt();
int startIdx = scan.nextInt();
visited = new boolean[nodeCnt + 1];
shortestPath = new int[nodeCnt + 1];
Arrays.fill(shortestPath, INF);
for(int i = 0; i <= nodeCnt; i++){
graph.add(new ArrayList<Node>());
}
// 간선 정보 입력 받기
for(int i = 0; i < edgeCnt; i++){
int node = scan.nextInt();
int target = scan.nextInt();
int distance = scan.nextInt();
graph.get(node).add(new Node(target, distance));
}
// 다익스트라 알고리즘 호출
dijkstra(startIdx);
Arrays.stream(shortestPath).skip(1).forEach(System.out::println);
}
// 다익스트라 알고리즘 수행
public static void dijkstra(int startIdx){
shortestPath[startIdx] = 0;
int now = startIdx;
while(now != 0){
visited[now] = true;
for(Node node : graph.get(now)){
if(shortestPath[node.getIndex()] > shortestPath[now] + node.getDistance()){
shortestPath[node.getIndex()] = shortestPath[now] + node.getDistance();
}
}
now = getSmallestNode();
}
}
// 다음 기준 노드 조회
public static int getSmallestNode(){
int min = 0;
for(int i = 1; i <= nodeCnt; i++){
if(!visited[i] && shortestPath[min] > shortestPath[i]){
min = i;
}
}
return min;
}
}
| 입력 예시 | 출력 예시 |
| 6 11 1 1 2 2 1 3 5 1 4 1 2 3 3 2 4 2 3 2 3 3 6 5 4 3 3 4 5 1 5 3 1 5 6 2 |
0 2 3 1 2 4 |
개선된 다익스트라 - 구현하기에는 조금 더 까다롭지만 빠르게 동작하는 코드
이 방법에서는 우선 순위 큐를 사용한다는 특징이 있다. 우선순위 큐는 우선순위가 가장 높은 데이터를 가장 먼저 삭제한다는 점이 있는 자료구조이다. 이 방법의 시간 복잡도는 노드의 개수가 V, 간선의 개수가 E일 때 O(ElogV)로 훨씬 빠르다.
import java.util.*;
class Node implements Comparable<Node> {
int index;
int distance;
public Node(int index, int distance){
this.index = index;
this.distance = distance;
}
public int getIndex() { return this.index; }
public int getDistance() { return this.distance; }
@Override
public int compareTo(Node node){
if(this.distance > node.getDistance()){
return 1;
}else if (this.distance < node.getDistance()){
return -1;
} else {
return 0;
}
}
}
public class Main
{
// 방문 정보 저장
private static boolean[] visited;
// 최단 거리 저장
private static int[] shortestPath;
// 간선 연결정보 저장
private static ArrayList<ArrayList<Node>> graph = new ArrayList<>();
// 무한대 값 상수
private static final int INF = (int) 1e9;
// 노드 개수
private static int nodeCnt;
// 간선 개수
private static int edgeCnt;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
nodeCnt = scan.nextInt();
edgeCnt = scan.nextInt();
int startIdx = scan.nextInt();
visited = new boolean[nodeCnt + 1];
shortestPath = new int[nodeCnt + 1];
Arrays.fill(shortestPath, INF);
for(int i = 0; i <= nodeCnt; i++){
graph.add(new ArrayList<Node>());
}
// 간선 정보 입력 받기
for(int i = 0; i < edgeCnt; i++){
int node = scan.nextInt();
int target = scan.nextInt();
int distance = scan.nextInt();
graph.get(node).add(new Node(target, distance));
}
// 다익스트라 알고리즘 호출
dijkstra(startIdx);
Arrays.stream(shortestPath).skip(1).forEach(System.out::println);
}
// 다익스트라 알고리즘 수행
public static void dijkstra(int startIdx){
// 최단 거리에 따른 우선순위 큐
private static PriorityQueue<Node> pQueue = new PriorityQueue<>();
shortestPath[startIdx] = 0;
pQueue.offer(new Node(startIdx, 0));
while(!pQueue.isEmpty()){
int now = pQueue.poll().getIndex();
visited[now] = true;
for(Node node : graph.get(now)){
if(shortestPath[node.getIndex()] > shortestPath[now] + node.getDistance()){
shortestPath[node.getIndex()] = shortestPath[now] + node.getDistance();
}
if(!visited[node.getIndex()]){
pQueue.offer(new Node(node.getIndex(), shortestPath[node.getIndex()]));
}
}
}
}
}
| 입력 예시 | 출력 예시 |
| 6 11 1 1 2 2 1 3 5 1 4 1 2 3 3 2 4 2 3 2 3 3 6 5 4 3 3 4 5 1 5 3 1 5 6 2 |
0 2 3 1 2 4 |
플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm)
모든 지점에서 모든 지점까지의 최단 경로를 모두 구해야하는 경우에 사용할 수 있는 알고리즘이다. 플로이드 워셜 알고리즘 또한 단계마다 '거쳐 가는 노드'를 기준으로 알고리즘을 수행한다. 하지만 매번 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다는 점이 다르다. 노드의 개수가 N일 때 알고리즘 상으로 N번의 단계를 수행하며, 단계마다 O(N²)의 연산을 통해 '현재 노드를 거쳐 가는' 모든 경로를 고려한다. 따라서 총 시간 복잡도는 O(N³)이다.
동작 과정은 아래 이미지로 자세히 알아볼 수 있다.
- 초기 상태: 그래프를 준비하고 최단 거리 테이블을 초기화한다.

- Step 1: 1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

- Step 2: 2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

- Step 3: 3번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

- Step 4: 4번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

플로이드 워셜 알고리즘 소스 코드
import java.util.*;
public class Main
{
// 무한대 값 상수
private static final int INF = (int) 1e9;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 노드 개수
int nodeCnt = scan.nextInt();
// 간선 개수
int edgeCnt = scan.nextInt();
// 최단 거리 저장
int[][] shortestPath = new int[nodeCnt + 1][nodeCnt + 1];
for(int[] row : shortestPath){
Arrays.fill(row, INF);
}
for(int i = 1; i <= nodeCnt; i++){
shortestPath[i][i] = 0;
}
// 간선 정보 입력 받기
for(int i = 0; i < edgeCnt; i++){
int node = scan.nextInt();
int target = scan.nextInt();
int distance = scan.nextInt();
shortestPath[node][target] = distance;
}
// 플로이드 워셜 알고리즘
for(int i = 1; i <= nodeCnt; i++){
for (int j = 1; j <= nodeCnt; j++){
for (int k = 1; k <= nodeCnt; k++){
if(i == j || i == k || j == k ) continue;
if(shortestPath[j][k] > shortestPath[j][i] + shortestPath[i][k]){
shortestPath[j][k] = shortestPath[j][i] + shortestPath[i][k];
}
}
}
}
// 결과 출력
for(int i = 1; i <= nodeCnt; i++){
for (int j = 1; j <= nodeCnt; j++){
System.out.print(String.format("%2d", shortestPath[i][j]) + " ");
}
System.out.println();
}
}
}| 입력 예시 | 출력 예시 |
| 4 7 1 2 4 1 4 6 2 1 3 2 3 7 3 1 5 3 4 4 4 3 2 |
0 4 8 6 3 0 7 9 5 9 0 4 7 11 2 0 |
예제 1 - 미래 도시
난이도 ●●○ | 풀이 시간 40분 | 시간 제한 1초 | 메모리 제한 128MB | M 기업 코딩 테스트
방문 판매원 A는 많은 회사가 모여 있는 공중 미래 도시에 있다. 공중미래 도시에는 1번부터 N번까지의 회사가 있는데 특정 회사끼리는 서로 도로를 통해 연결되어 있다. 방문 판매원 A는 현재 1번 회사에 위치해 있으며, X번 회사에 방문해 물건을 판매하고자 한다.
공중 미래 도시에서 특정 회사에 도착하기 위한 방법은 회사끼리 연결되어 있는 도로를 이용하는 방법이 유일하다. 또한 연결된 2개의 회사는 양방향으로 이동할 수 있다. 공중 미래 도시에서의 도로는 마하의 속도로 사람을 이동시켜 주기 때문에 특정 회사와 다른 회사가 도로로 연결되어 있다면, 정확히 1만큼의 시간으로 이동할 수 있다.
또한 오늘 방문 판매원 A는 기대하던 소개팅에도 참석하고자 한다. 소개팅의 상대는 K번 회사에 존재한다. 방문 판매원 A는 X번 회사에 가서 물건을 판매하기 전에 먼저 소개팅 상대의 회사에 찾아가서 함께 커피를 마실 예정이다. 따라서 방문 판매원 A는 1번 회사에서 출발하여 K번 회사를 방문한 뒤에 X번 회사로 가는 것이 목표다. 이때 방문 판매원 A는 가능한 한 빠르게 이동하고자 한다.
방문 판매원이 회사 사이를 이동하게 되는 최소 시간을 계산하는 프로그램을 작성하시오. 이때 소개팅의 상대방과 커피를 마시는 시간 등은 고려하지 않는다고 가정한다.
입력 조건
- 첫째 줄에 전체 회사의 개수 N과 경로의 개수 M이 공백으로 구분되어 차례대로 주어진다. (1 <= N, M <= 100)
- 둘째 줄부터 M + 1 번째 줄에는 연결된 두 회사의 번호가 공백으로 구분되어 주어진다.
- M + 2번째 줄에는 X와 K가 공백으로 구분되어 차례대로 주어진다. (1 <= K <= 100)
출력 조건
- 첫째 줄에 방문 판매원 A가 K번 회사를 거쳐 X번 회사로 가는 최소 이동 시간을 출력한다.
- 만약 X번 회사에 도달할 수 없다면 -1을 출력한다.
입력/출력 예시
| 입력 예시 | 출력 예시 |
| 5 7 1 2 1 3 1 4 2 4 3 4 3 5 4 5 4 5 |
3 |
| 4 2 1 3 2 4 3 4 |
-1 |
요점
- 전형적인 플로이드 워셜 알고리즘 문제이며 N의 범위도 100 이하로 매우 한정적이다.
- 원하는 결과는 (1번 노드에서 X까지의 최단 거리 + X에서 K까지의 최단 거리)이다.
소스 코드
import java.util.*;
public class Main
{
// 무한대 값 상수
private static final int INF = (int) 1e9;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int campanyCnt = scan.nextInt();
int roadCnt = scan.nextInt();
// 최단 거리 저장
int[][] shortestPath = new int[campanyCnt + 1][campanyCnt + 1];
for(int[] row : shortestPath){
Arrays.fill(row, INF);
}
for(int i = 1; i <= campanyCnt; i++){
shortestPath[i][i] = 0;
}
// 간선 정보 입력 받기
for(int i = 0; i < roadCnt; i++){
int companyA = scan.nextInt();
int companyB = scan.nextInt();
shortestPath[companyA][companyB] = 1;
shortestPath[companyB][companyA] = 1;
}
int second = scan.nextInt();
int first = scan.nextInt();
// 플로이드 워셜 알고리즘
for(int i = 1; i <= campanyCnt; i++){
for (int j = 1; j <= campanyCnt; j++){
for (int k = 1; k <= campanyCnt; k++){
if(i == j || i == k || j == k ) continue;
if(shortestPath[j][k] > shortestPath[j][i] + shortestPath[i][k]){
shortestPath[j][k] = shortestPath[j][i] + shortestPath[i][k];
}
}
}
}
int result = shortestPath[1][first] + shortestPath[first][second];
result = result >= INF ? -1 : result;
System.out.println("result = " + result);
}
}
예제 2 - 전보
난이도 ●●● | 풀이 시간 60분 | 시간 제한 1초 | 메모리 제한 128MB | 유명 알고리즘 대회
어떤 나라에는 N개의 도시가 있다. 그리고 각 도시는 보내고자 하는 메시지가 있는 경우, 다른 도시로 전보를 보내서 다른 도시로 해당 메시지를 전송할 수 있다. 하지만 X라는 도시에서 Y라는 도시로 전보를 보내고자 한다면, 도시 X에서 Y로 향하는 통로가 설치되어 있어야 한다. 예를 들어 X에서 Y로 향하는 통로는 있지만, Y에서 X로 향하는 통로가 없다면 Y는 X로 메시지를 보낼 수 없다. 또한 통로를 거쳐 메시지를 보낼 때는 일정 시간이 소요된다.
어느 날 C라는 도시에서 위급 상황이 발생했다. 그래서 최대한 많은 도시로 메시지를 보내고자 한다. 메시지는 도시 C에서 출발하여 각 도시 사이에 설치된 통로를 거쳐, 최대한 많이 퍼져나갈 것이다. 각 도시의 번호와 통로가 설치되어 있는 정보가 주어졌을 때, 도시 C에서 보낸 메시지를 받게 되는 도시의 개수는 총 몇 개이며 도시들이 모두 메시지를 받는 데까지 걸리는 시간은 얼마인지 계산하는 프로그램을 작성하시오.
입력 조건
- 첫째 줄에 도시의 개수 N, 통로의 개수 M, 메시지를 보내고자 하는 도시 C가 주어진다.
(1 <= N <= 30,000, 1 <= M <= 200,000, 1 <= C <= N) - 둘째 줄부터 M + 1번째 줄에 걸쳐서 통로에 대한 정보 X, Y, Z가 주어진다. 이는 특정 도시 X에서 다른 특정 도시 Y로 이어지는 통로가 있으며, 메시지가 전달되는 시간이 Z라는 의미다.
(1 <= X, Y <= N, 1 <= Z <= 1,000)
출력 조건
- 첫째 줄에 도시 C에서 보낸 메시지를 받는 도시의 총 개수와 총 걸리는 시간을 공백으로 구분하여 출력한다.
입력/출력 예시
| 입력 예시 | 출력 예시 |
| 3 2 1 1 2 4 1 3 2 |
2 4 |
요점
- 한 도시에서 다른 도시까지의 최단 거리 문제로 다익스트라 알고리즘을 이용해서 풀 수 있다.
- N과 M의 범위가 크기 떄문에 우선순위 큐를 이용해서 다익스트라 알고리즘을 작성해야한다.
소스 코드
import java.util.*;
class City implements Comparable<City> {
int index;
int time;
public City(int index, int time){
this.index = index;
this.time = time;
}
public int getIndex() { return this.index; }
public int getTime() { return this.time; }
@Override
public int compareTo(City city){
if(this.time > city.getTime()){
return 1;
}else if (this.time < city.getTime()){
return -1;
} else {
return 0;
}
}
}
public class Main
{
private static final int INF = (int) 1e9;
private static int cityCnt;
private static int pathCnt;
private static int startCity;
private static int[] shortestPath;
private static boolean[] visited;
private static ArrayList<ArrayList<City>> paths = new ArrayList<>();
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
cityCnt = scan.nextInt();
pathCnt = scan.nextInt();
startCity = scan.nextInt();
visited = new boolean[cityCnt + 1];
shortestPath = new int[cityCnt + 1];
Arrays.fill(shortestPath, INF);
for(int i = 0; i <= cityCnt; i++){
paths.add(new ArrayList<City>());
}
for(int i = 0; i < pathCnt; i++){
int cityA = scan.nextInt();
int cityB = scan.nextInt();
int time = scan.nextInt();
paths.get(cityA).add(new City(cityB, time));
}
dijkstra();
int count = 0;
int maxTime = 0;
for (int i = 1; i <= cityCnt; i++) {
if (shortestPath[i] != INF && i != startCity) {
count += 1;
maxTime = Math.max(maxTime, shortestPath[i]);
}
}
System.out.println("result = " + count + " " + maxTime);
}
public static void dijkstra(){
PriorityQueue<City> qQueue = new PriorityQueue<>();
shortestPath[startCity] = 0;
qQueue.offer(new City(startCity, 0));
while(!qQueue.isEmpty()){
int now = qQueue.poll().getIndex();
visited[now] = true;
for(City dest : paths.get(now)){
if(shortestPath[dest.getIndex()] > shortestPath[now] + dest.getTime()){
shortestPath[dest.getIndex()] = shortestPath[now] + dest.getTime();
}
if(!visited[dest.getIndex()]){
qQueue.offer(new City(dest.getIndex(), shortestPath[dest.getIndex()]));
}
}
}
}
}
최단 경로 예제를 풀어본 후
어제 풀어본 다이나믹 알고리즘이 워낙 나에겐 어려웠어서 그런지 최단 거리 알고리즘은 비교적 이해하는데 어려움이 없었던 것 같다. 그런데 이런 암기가 필요한 알고리즘은 지금은 이해하고 작성해도 다음에 작성하려면 헤매게 되는 게 단점이다ㅜㅜ 다음에도 지금처럼 잘 기억하고 있으면 좋을 텐데 시간 날 때마다 틈틈이 복습을 해야겠다.
GitHub: https://github.com/Leeyeonjae/coding-test/tree/main/9_ShortestPath
참고서적 : 이것이 취업을 위한 코딩 테스트다 with 파이썬 by 나동빈
